Jednołącznikowy falownik napięciowy klasy E w zastosowaniu do nagrzewania indukcyjnego – topologia, cykle pracy oraz koncepcja sterowania modelu układu

W celu weryfikacji otrzymanych wyników zastosowano następnie metodę oporów magnetycznych[7]. Podstawą do budowy schematu zastępczego jest analiza rozpływu strumieni magnetycznych w układzie wzbudnik – wsad.

Schemat zastępczy indukcyjnego układu grzejnego da tej metody przedstawiono na rys. 7, zaś wyniki obliczeń w tab. 3.

Rys. 7. Schemat zastępczy dla metody oporów magnetycznych

Wielkości X_Δ i X₂ reprezentują reluktancje związanie odpowiednio ze strumieniem rozproszenia Φ_Δ przenikającym szczelinę powietrzną pomiędzy wsadem a wzbudnikiem oraz strumieniem Φ₂ przenikającym wsad. Rezystancja R₂ to rezystancja wnoszona przez wsad, zaś reaktancja X₀ jest związana z głównym strumieniem magnetycznym Φ.

Tab. 3. Wyniki obliczeń metodą oporów magnetycznych:

Ponieważ obliczenia dotyczące parametrów schematu zastępczego znacznie się różnią w przypadku dwóch użytych metod (zwłaszcza wartość rezystancji zastępczej układu), do dalszej weryfikacji zastosowano trzecią metodę transformatora powietrznego [7]. W metodzie tej wsad zastępowany jest zwojem zwartym. Uzwojenia wzbudnika oraz zwój zwarty tworzą wówczas transformator powietrzny w stanie zwarcia, przy czym liczba zwojów uzwojenia wtórnego wynosi: w₂ = 1.

Schematy zastępcze układu grzejnego wzbudnik – wsad dla metody transformatora powietrznego przedstawiono na rys. 8, a wyniki obliczeń podano w tab. 4. Występujący w niej współczynnik p₁₂ zależy od wymiarów oraz parametrów wzbudnika i wsadu [7].

Rys. 8. Schematy zastępcze układu grzejnego wzbudnik-wsad dla metody transformatora powietrznego

Tab. 4. Wyniki obliczeń metodą transformatora powietrznego:

Obliczenie parametrów wykonanego wzbudnika na podstawie jego gabarytów zewnętrznych nie jest proste, a otrzymane wyniki w zależności od użytej metody bardzo się od siebie różnią. Konieczne jest jednak wstępne przyjęcie wartości wyjściowych takiej konstrukcji w celu symulacji układu zmierzającej do weryfikacji jego warunków pracy i wypracowania metod, które pozwolą optymalnie sterować urządzeniem.

Metoda oporów wniesionych jest wystarczająco dokładna dla wsadów długich. Zależności określające wielkości parametrów zostały wyprowadzone dla układu o nieskończonej długości, a ich skończoną długość koryguje się następnie za pomocą współczynników korekcyjnych. Niedokładność metody jest związana z założeniami, iż linie pola elektromagnetycznego są prostopadłe do wsadu (pomija się warunki brzegowe), co w przypadku układów relatywnie krótkich wyraźnie pogarsza wiarygodność obliczeń, nawet pomimo zastosowania współczynników korekcyjnych.

Metoda oporów magnetycznych ma zastosowanie przede wszystkim do obliczania układów grzejnych z wsadami magnetycznymi. Jednocześnie jest stosowana do obliczeń układów grzejnych o skończonych wymiarach. Należy do najczęściej stosowanych sposobów obliczeniowych, dając zwykle dobre przybliżenia wartości rzeczywistych.

Natomiast metoda transformatora powietrznego jest stosowana przede wszystkim do obliczeń układów grzejnych z wsadami niemagnetycznymi o skończonych wymiarach. Należy do najczęściej stosowanych metod, dając również dobre przybliżenia parametrów rzeczywistych układu wzbudnik – wsad. Należy przy tym pamiętać, że w analizowanym przypadku:

• wzbudnik wykonano z okrągłej rurki, a obliczenia są dokładniejsze dla rurki o przekroju prostokątnym,
• wsad wystaje poza wzbudnik, ale nie jest wielokrotnie dłuższy od wzbudnika, jak podaje [7], mówiąc o nagrzewaniu miejscowym,
• głębokość wnikania pola elektromagnetycznego do wsadu jest bardzo mała i nie jest to częstotliwość właściwa dla nagrzewania skrośnego tego wsadu; przykładowo współczynnik χ2 dla wsadu zimnego wynosi ok. 80, a w [7, tabl. V] jego zakres jest tylko do 20,
• ogromną trudność sprawia dokładne określenie przenikalności magnetycznej względnej μr stali z której wykonany jest wsad, a który ma kluczowe znaczenie dla tłumienia w układzie rezonansowym i tym samym generacji ciepła; wartości przenikalności μr dla stali mogą się wahać w granicach: od jedności (μr dla stali zwykłej w temperaturze 800°C; μr = 16 dla tej samej stali zwykłej w temperaturze 20°C), do wartości wielu tysięcy (izotropowa stal elektrotechniczna (Fe₉₆Si₄) – 7000; anizotropowa stal elektrotechniczna (Fe₉₇Si₃) – 100000).

W związku z powyższymi właściwościami metod obliczeniowych oraz mając na uwadze powyższe nieścisłości, do dalszych rozważań i symulacji, przyjęto wstępnie uśrednione wartości obliczonych parametrów rezystancji zastępczej odbiornika R₀, reaktancji zastępczej odbiornika X₀ i indukcyjności zastępczej odbiornika L₀ dla temperatur: 20°C i 800°C, przy założonej częstotliwości prądu odbiornika równej f = 470 kHz. 

Tab. 5. Zestawienie wyników obliczeń:

Symulacja pracy falownika w pakiecie IsSpice 

Uzyskane drogą symulacji w programie IsSpice przebiegi prądów i napięć w falowniku przy pracy optymalnej i przyjęciu średnich wartości parametrów z tab. 5 dla 20°C przedstawiono na rys. 9. Po przyjęciu pojemności kondensatora C równej 0,42 μF symulowany obwód można scharakteryzować dobrocią Q (daną zależnością 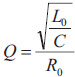 ), wynoszącą 4,86. W symulacji wykorzystano bibliotekę tranzystora IRFP260, którego użyto w konstrukcji modelu układu. Maksymalne napięcie na kondensatorze przekracza ok. 2,5-krotnie wartość napięcia zasilania U_d.

Rys. 9. Przebiegi prądu i_T tranzystora, napięcia u_T na tranzystorze, prądu i₀ wzbudnika oraz napięcia u_C na kondensatorze C dla falownika o średnich wartościach parametrów z tab. 5 przy 20°C (co odpowiada Q = 4,86) oraz C = 0,42 μF, U_d = 40 V; fs = 485 kHz 

Dla zobrazowania wpływu tłumienia obwodu rezonansowego na przebiegi prądów i napięć na rys. 10 i 11 przedstawiono przebiegi prądów i napięć w falowniku dla obwodów o innych wartościach tłumienia. Widoczny jest znaczny wzrost odkształcenia prądu odbiornika przy zwiększaniu tłumienia obwodu.

Podsumowanie

Analizowany w pracy falownik może pracować optymalnie w klasie E pod warunkiem, że dobroć obwodu szeregowego R₀L₀C jest wystarczająco duża (Q > ok. 2,61).

Regulacja mocy falownika pracującego optymalnie jest możliwa przez zmianę napięcia zasilania. Alternatywą jest odejście od pracy optymalnej przez odpowiednie zwiększenie czasu przewodzenia tranzystora i okresu jego przełączania, co skutkuje zwiększeniem mocy falownika przy zachowaniu przełączania ZVS. Możliwym rozwiązaniem regulacji mocy jest także wydłużenie taktu II-go pracy falownika i dopuszczenie w układzie do wielokrotności przeładowań w obwodzie rezonansowym R₀L₀C.

Wymaga to jednak użycia łączników bez diody zwrotnej. Taki sposób regulacji pozwala wyłącznie na obniżenie mocy wyjściowej urządzenia. Zaletą omawianego falownika jest zastosowanie tylko jednego zaworu energoelektronicznego, a wadą – duża wartość napięcia na łączniku przy dużym tłumieniu w obwodzie rezonansowym (np. ze wsadem ze stali ferromagnetycznej). Wada ta staje się jednak mniej istotna w przypadku zastosowania zaworu nowej generacji, np. wykonanego w technologii SiC. 

Rys. 10. Przebiegi prądu iT tranzystora, napięcia u_T na tranzystorze, prądu i₀ wzbudnika oraz napięcia u_C na kondensatorze C dla przykładowego obwodu o mniejszym tłumieniu (Q = 9,87) oraz U_d = 40 V; f_s = 361 kHz

Rys. 11. Przebiegi prądu i_T tranzystora, napięcia u_T na tranzystorze, prądu i₀ wzbudnika oraz napięcia u_C na kondensatorze C dla przykładowego obwodu o większym tłumieniu (Q = 2,8531) oraz U_d = 40 V; f_s = 222 kHz

Literatura:

[1] Omori H., Yamashita H., Nakaoka M., Maruhashi T.: A Novel Type Induction-Heating Single-Ended Resonant Inverter Using New Bipolar Darlington-Transistor. IEEE Power Electronics Specialist Conference Rec., 1985, Vol. 1, pp. 590–599.

[2] Llorente S., Monterde F., Burdío J.M., Acero J.: A Comparative Study of Resonant Inverter Topologies Used in Induction Cookers, Applied Power Electronics Conference and Exposition, APEC 2002, Vol. 2, pp. 1168–1174.

[3] Saoudi M.; Puyal D.; Bernal C.; Antón, D.; Mediano, A.: Induction Cooking Systems with Single Switch Inverter Using New Driving Techniques, Industrial Electronics (ISIE), 2010 IEEE International Symposium on, vol. no. 4–7 July 2010, pp. 878–883.

[4] Jednołącznikowy falownik z przełączaniem ZVS do nagrzewania indukcyjnego – praca optymalna. Referat wygłoszony na Konferencji: Problemy Cieplne w Elektrotechnice i Elektrotechnologie, Konopnica, wrzesień 2013.

[5] Kaczmarczyk Z.: Falownik klasy E – teoria i praktyka przekształtnika wysokiej częstotliwości. Przegląd Elektrotechniczny nr 9/2004.

[6] Citko T., Tunia H., Winiarski B.: Układy rezonansowe w energoelektronice. Seria Postępy Napędu Elektrycznego i Energoelektroniki. Wydawnictwo Politechniki Białostockiej 2001 r.

[7] Sajdak Cz., Samek E.: Nagrzewanie indukcyjne. Podstawy teoretyczne i zastosowanie. Wydawnictwo „Śląsk”, Katowice 1985.

[8] A ndrew Livesey, Alan Robinson: Repair of vehicle bodies. Amsterdam: Elsevier, Butterworth-Heinemann, 2006, s. 166. ISBN 978-0-7506-6753-1.

[9] CRC Handbook of Chemistry and Physics, 83-th ed.; s. 12–204; CRC Press LLC: Boca Raton, 2003.