FDP Butterwortha ( projektowanie, charakterystyki czasowe i częstotliwościowe )

Przy pomocy programu Matlab w wersji 6.5 wyznaczam charakterystyki amplitudowe i fazowe zaprojektowanego filtru dolnoprzepustowego typu Butterwortha. Zamieszczam również komendy zastosowane w programie Matlab.

l=[1 4 6 4 1];
m=[1.2492741213799666264 -4.4421205821121396861 5.9506837076443589775 -3.5574567543760017083 0.80046483448753300182];
a=0.52832938982325704646e-4;

freqz([l]*a,[m],0:1:1000,48000),figure,freqz([l]*a,[m],999.9:0.01:1000.1,48000),figure,freqz([l]*a,[m],0:1:6000,48000),figure,freqz([l]*a,[m],5499:0.1:5501,48000)

Płaska charakterystyka w paśmie przepustowym

Tłumienie na końcu pasma przepustowego

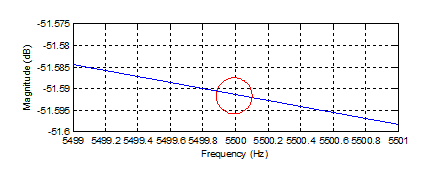
Oczywiście dla postaci znormalizowanej i kaskadowej charakterystyki są analogiczne z prezentowanymi powyżej. Filtr idealnie realizuje założenia projektowe m.in. ma płaską charakterystykę częstotliwościową w paśmie przepustowym. Dodatkowo przy częstotliwości 1000Hz tłumienie wynosi dokładnie 0.5dB a przy 5500Hz, gdzie zaczyna się pasmo zaporowe, tłumienie filtru osiąga wartość większą niż 51dB – jest większe o ponad 3dB od założonego co jest zjawiskiem pozytywnym ponieważ w paśmie zaporowym filtr tłumi sygnały lepiej niż to założyliśmy. Spowodowane jest to tym, że wyliczony rząd filtru nie jest wartością całkowitą. Do potrzeb projektowych zaokrąglamy tą wartość w górę. Ponadto przeliczenie częstotliwości granicznej dokonaliśmy za pomocą wzoru z dokładnym punktem (A_p,f_p) co jest przyczyną takiego przebiegu charakterystyk.
Przeliczając częstotliwość graniczną względem punktu (A_r,f_r) uzyskuję dokładną wartość tłumienia założonego przy częstotliwości 5500Hz gdzie zaczyna się pasmo zaporowe. W stworzonym arkuszu programu mathcad przeliczam częstotliwość graniczną względem punktu (A_r,f_r).

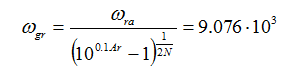
Poniżej prezentuję efekty dokonanego przeliczenia transmitancji.

Współczynniki transmitancji oraz ich dokładne wartości

Wartości dokładne:
współczynnik licznika
              0.79887511848703919826e^-4

współczynnik mianownika
               1.2798514410632130843
               -4.4893587866007203332
               5.9394469703326580220
               -3.5100021133044900354
               0.78134068869891852488

Poniżej prezentuję charakterystyki częstotliwościowe omawianego wyżej filtru

l=[1 4 6 4 1];
a=.79887511848703919826e-4;
m=[1.2798514410632130843 -4.4893587866007203332 5.9394469703326580220 -3.5100021133044900354 .78134068869891852488];

freqz([l]*a,[m],999:0.1:1001,48000),figure,freqz([l]*a,[m],5499:0.1:5501,48000);

Jak widać sprawdziły się moje oczekiwania. Przy wyznaczeniu częstotliwości granicznej z dokładnym punktem (A_r,f_r) amplitudowa charakterystyka częstotliwościowa przy 5500Hz osiąga wartości dokładnie -48dB. Natomiast taki filtr nie zapewniałby odpowiednio silnego tłumienia na końcu założonego pasma przepustowego przy częstotliwości 1000Hz.

Do dalszych rozważań będę się opierał przy filtrze, w którym częstotliwość graniczna była wyznaczona z dokładnym punktem (A_p,f_p)