

Teoria szeregowania i alokacji zadań obecnie rozwijana jest równolegle przez badaczy działających w ramach dwóch różnych dyscyplin naukowych, do których zaliczają się badania operacyjne oraz architektury systemów komputerowych. W przypadku drugiej z wymienionych gałęzi wiedzy zasadniczym celem jest wskazanie miejsca wykonywania zadań obliczeniowych, tzn. określenie, do której jednostki obliczeniowej zostaną przydzielone, oraz wyznaczenie czasu rozpoczęcia i zakończenia ich realizacji [1].
Teoria szeregowania zadań nabiera szczególnego znaczenia w kontekście komputerowych systemów sterujących, a zwłaszcza systemów czasu rzeczywistego o ostrych ograniczeniach czasowych (ang. hard real-time), w przypadku których naruszenie ograniczenia czasowego dowolnego z zadań obliczeniowych prowadzić może do trudnych do oszacowania skutków, będących następstwami powstania poważnej awarii, katastrofy, wielkich strat finansowych, a nawet zagrożenia życia ludzkiego [2]. Ponieważ obecnie systemy czasu rzeczywistego spotykane są praktycznie w każdym obszarze technicznej działalności człowieka, a zwłaszcza w energetyce, telekomunikacji, transporcie, inżynierii biomedycznej i zautomatyzowanych systemach produkcyjnych, kwestie bezpieczeństwa pracy tego typu systemów nabierają szczególnego znaczenia [3].
Ponieważ w przypadku komputerowych systemów sterujących w żadnym wypadku nie można pozwolić sobie na przeprowadzane w warunkach rzeczywistych eksperymenty, które mogłyby nieść ze sobą pewne katastrofalne następstwa, zatem pozostaje jedynie wykorzystanie dostępnych metod formalnych i wykazanie już samym etapie projektu systemu, że w każdych możliwych warunkach jego pracy każde z wykonywanych zadań obliczeniowych zawsze dochowa swego ograniczenia czasowego [4]. Jest to niezmiernie ważne, jeśli weźmie się pod uwagę, że w przypadku systemu czasu rzeczywistego uzyskanie poprawnych wyników, pod względem ich analizy logicznej, lecz spóźnionych, jest całkowicie bezużyteczne, ponieważ w przypadku naruszenia ograniczenia czasowego zadania sterowany proces wymyka się zwykle spod dalszej kontroli i często nie jesteśmy już w stanie jego niekontrolowanego przebiegu opanować, co w wielu przypadkach może nieść ze sobą niezwykle poważne katastrofalne następstwa [5].
Już na wstępnie należy nadmienić, że nie istnieją żadne uniwersalne algorytmy szeregowania zadań, które byłyby odpowiednie w przypadku dowolnego typu zadań. Natomiast wyróżnia się odrębne klasy algorytmów szeregowania, które są przeznaczone do szeregowania różnego typu zadań [6]. Najczęściej prowadzona linia podziału przebiega pomiędzy zadaniami okresowymi i aperiodycznymi. Również odrębne klasy algorytmów szeregujących stosuje się w przypadku zadań wywłaszczalnych i niewywłaszczalnych [7]. Także wyróżnia się odrębne algorytmy przewidziane do szeregowania zadań zależnych i niezależnych. Natomiast odmienna płaszczyzna podziału przebiega pomiędzy algorytmami przewidzianymi do szeregowania zadań jednoprocesorowych i wieloprocesorowych, przy czym te drugie dzielą się na zadania przeznaczone dla procesorów arbitralnych lub dedykowanych [8].
W przypadku komputerowych systemów sterujących najczęściej występującym typem zadań są zadania periodyczne, niezależne i wywłaszczalne przeznaczone do realizacji na pojedynczym procesorze. Niezwykle popularnym algorytmem przewidzianym do szeregowania rozważanego typu zadań jest algorytm Rate Monotonic Scheduling, który został zaimplementowany w przypadku zdecydowanej większości systemów operacyjnych czasu rzeczywistego. Dlatego w kolejnym punkcie opisano w skróciejego najważniejsze właściwości.
Algorytm Rate Monotonic Scheduling w swej klasycznej postaci przeznaczony jest do szeregowania zbioru zadań periodycznych, niezależnych i wywłaszczalnych, wykonywanych na pojedynczym procesorze. Każde tego typu zadanie charakteryzowane jest przez czas swego wykonywania C (rozpatrywany zazwyczaj jako czas wykonywania dla najgorszego z możliwych przypadków) oraz okres T. Jednocześnie wartość stosunku C/T wyznacza stopień wykorzystania procesora przez dane zadanie periodyczne [9].
Rozważany algorytm szeregowania zadań periodycznych bazuje na systemie priorytetów, które przypisywane są w sposób statyczny do poszczególnych zadań, przy czym obowiązuje zasada, że zadanie o mniejszej wartości okresu, czyli takie, które jest aktywowane częściej, otrzymuje wyższy priorytet. W dowolnym momencie procesor spośród wszystkich zadań znajdujących się w stanie gotowości realizuje właśnie to, które ma najwyższy priorytet. Jeżeli w trakcie wykonywania takiego zadania w stan gotowości wejdzie jakieś inne zadanie o jeszcze wyższym priorytecie, wówczas aktualnie wykonywane zadanie zostanie wywłaszczone, a procesor zostanie przekazany do realizacji nowo przybyłego zadania. Ponadto zadanie, które uległo wywłaszczeniu, będzie mogło zostać wznowione dopiero w sytuacji, gdy w stanie gotowości nie będzie znajdowało się już żadne inne zadanie o wyższym priorytecie.
Jest rzeczą oczywistą, że w przypadku szeregowania zbioru N periodycznych, niezależnych i wywłaszczalnych zadań stopień wykorzystania procesora przez szeregowane zadania nie może przekraczać jedności, co stanowi tzw. warunek konieczny na szeregowalność zbioru zadań, który określony jest następującą nierównością (1)
W tym miejscu trzeba zaznaczyć, że spełnienie warunku koniecznego wcale jeszcze nie stanowi gwarancji, że dany zbiór zadań periodycznych będzie szeregowalny. Gwarancję taką może udzielić jedynie warunek wystarczający na szeregowalność zbioru zadań, który zadany jest następującą nierównością (2)
Dla dużej liczby zadań N prawa strona nierówności dość szybko zmierza w sposób asymptotyczny do wartości równej ln2, czyli około 0,693. Zatem w praktyce można przyjąć, i to już w przypadku szeregowania zbioru zawierającego kilka zadań periodycznych, że zbiór ten jest zawsze szeregowalny za pomocą algorytmu Rate Monotonic Scheduling w sytuacji, gdy stopień wykorzystania przez niego procesora nie przekracza wartości 0,693.
Natomiast w przypadku, gdy spełniony jest warunek konieczny (1), a jednocześnie nie jest spełniony warunek wystarczający (2), to w pewnych wypadkach dany zbiór zadań może być nadal szeregowalny. Aby to sprawdzić, należy rozważyć najgorszy z możliwych przypadków, czyli taki, w którym wszystkie zadania podlegające procesowi szeregowania wchodzą jednocześnie w stan gotowości. Wówczas zadanie o najniższym priorytecie będzie mogło rozpocząć swoje wykonywanie dopiero wtedy, gdy wszystkie pozostałe zadania periodyczne zostaną wykonane przynajmniej jeden raz. Analizując najgorszy z możliwych przypadków, należy wykazać dla każdego z szeregowanych zadań, że zostanie zakończone przed upływem jego ograniczenia czasowego. Dopiero gdy powyższy warunek jest spełniony, można uznać, że dany zbiór zadań jest szeregowalny.
W przypadku praktycznych implementacji komputerowych systemów sterujących istotny problem stanowi precyzyjne oszacowanie czasu wykonywania zadania periodycznego C. Niestety w wielu wypadkach czas ten nie jest dokładnie znany, choćby z tego względu, że jest on zależny (zwykle w bardzo uwikłany sposób) od postaci danych wejściowych przetwarzanych przez rozważane zadanie, w związku z czym dwie kolejne realizacje tego samego zadania mogą znacznie się różnić czasem swego wykonywania. W związku z tym, w celu policzenia wartości lewej strony nierówności (2), należy w przypadku każdego z szeregowanych zadań jako wartość czasu wykonania C przyjąć wartość wyliczoną dla najgorszego z możliwych przypadków. Niestety precyzyjne wyznaczenie najdłuższego z możliwych czasów realizacji danego zadania nie zawsze jest możliwe do uzyskania na drodze rozważań formalnych i w praktyce podlega zazwyczaj jedynie pewnemu oszacowaniu (poprzez wykonanie odpowiednio dużej liczby testów) z dodatkowym uwzględnieniem odpowiedniego marginesu bezpieczeństwa. Jednak taka metoda postępowania nie daje żadnej gwarancji, że w pewnych szczególnych przypadkach czas realizacji zadania C nie będzie istotnie dłuższy, niż pierwotnie przyjęto. W związku z powyższym nie jest bynajmniej rzeczą dobrą obciążać procesor w stopniu większym, niż wynika to z warunku wystarczającego (2), ponieważ jedynie obciążenie procesora w stopniu mniejszym niż około 0,693 daje stosowny margines bezpieczeństwa na wypadek, gdyby któreś z zadań przekroczyło wyznaczony w jego przypadku czas wykonywania C.
W sytuacji, gdy liczba szeregowanych zadań N jest duża, może się tak zdarzyć, że warunek wystarczający (2) nie będzie mógł być spełniony, nawet w przypadku zastosowania procesora o największej z dostępnych mocy obliczeniowych, który byłby w stanie zagwarantować dla każdego z realizowanych zadań możliwie najkrótszy czas jego wykonywania C. Taka sytuacja w przypadku współczesnych komputerowych systemów sterujących jest nader częsta, a liczba różnego typu sensorów dostarczających sygnałów ze sterowanego obiektu w nowoczesnych implementacjach nieustannie wzrasta. Dla przykładu można podać tylko, że w przypadku nowoczesnego bloku energetycznego o mocy kilkuset megawatów stan jego pracy monitorowany jest w czasie rzeczywistym za pomocą kilkudziesięciu tysięcy różnego typu czujników. W rozważanym przypadku jest rzeczą oczywistą, że takie gigantyczne wręcz ilości danych nie mogą zostać przetworzone z zachowaniem reżimów czasu rzeczywistego za pomocą tylko jednego procesora, w związku z czym zastosowanie systemu wieloprocesorowego staje się koniecznością [10].
Stosując system wieloprocesorowy w celu realizacji za jego pomocą zbioru N zadań periodycznych, które szeregowane są z wykorzystaniem algorytmu Rate Monotonic Scheduling, w przypadku każdego z procesorów należy zagwarantować, że przydzielony do niego podzbiór zadań spełniał będzie warunek wystarczający na jego szeregowalność (2). Dodatkowo do dobrej praktyki należy dokonanie takiej alokacji zadań, która zapewni w miarę równomierne obciążenie poszczególnych procesorów systemu.
Ponadto pamiętać należy, że wszelkie systemy wieloprocesorowe dzielą się na dwie odrębne kategorie systemów homogenicznych i heterogenicznych. W przypadku systemów homogenicznych wszystkie procesory wchodzące w ich skład są jednakowe, natomiast w przypadku systemów heterogenicznych wchodzące w ich skład procesory odznaczają się już zróżnicowanymi poziomami mocy obliczeniowej. W tym kontekście podanych definicji można dodatkowo traktować systemy heterogeniczne jako pewną szerszą kategorię systemów wieloprocesorowych, w skład której wchodzą również systemy homogeniczne, traktowane jako pewien szczególny przypadek, w którym moce obliczeniowe wszystkich procesorów są równe.
W przypadku większej liczby zadań N znalezienie optymalnego schematu ich alokacji do poszczególnych procesorów nie jest realizowalne w praktyce metodą przeglądu zupełnego, ponieważ czas koniecznych do przeprowadzenia w tym celu obliczeń rośnie wykładniczo wraz z liczbą alokowanych zadań. Dodatkowo przypadek systemu heterogenicznego, w którym każdy z procesorów odznacza się innym poziomem mocy obliczeniowej, dodatkowo komplikuje obliczenia. Z tego powodu autor zdecydował się na zastosowanie techniki obliczeniowej opartej na algorytmach ewolucyjnych w celu poszukiwania suboptymalnych schematów alokacji zadań do poszczególnych procesorów w przypadku zastosowania heterogenicznych systemów wieloprocesorowych, które byłyby w stanie zagwarantować spełnienie w przypadku każdego z procesorów warunku wystarczającego na szeregowalność przydzielonego o niego podzbioru zadań oraz zapewnić równomierny stopień obciążenia poszczególnych procesorów wchodzących w skład rozważanego systemu.
W celu zilustrowania sposobu implementacji algorytmu ewolucyjnego na potrzeby realizacji zadania alokacji zadań periodycznych w heterogenicznym systemie wieloprocesorowym rozważono przykładowy system zbudowany z pięciu procesorów charakteryzujących się zróżnicowanym poziomem mocy obliczeniowej. Założono, że procesor nr 1 odznacza się największą mocą obliczeniową, której poziom określono jako 100%, co zarazem stanowi poziom odniesienia dla mocy obliczeniowych pozostałych procesorów. Z kolei moc obliczeniowa procesora nr 2 została ustalona na 90% rozważanego poziomu odniesienia mocy obliczeniowej. Analogicznie przyjęto, że moc obliczeniowa procesora nr 3 wynosi 85%, moc obliczeniowa procesora nr 4 wynosi 80%, a moc obliczeniowa procesora nr 5 wynosi 75% ustalonego poziomu odniesienia mocy obliczeniowej. W związku z powyższym czasy realizacji zadań, które zostały podane dla procesora nr 1, w przypadku pozostałych procesorów, odznaczających się niższym poziomem mocy obliczeniowej, będą proporcjonalnie dłuższe.
Aby można było zastosować algorytm ewolucyjny w celu optymalizacji przydziału zadań periodycznych do poszczególnych procesorów rozważanego systemu heterogenicznego należy na wstępie określić dwie kwestie. Pierwszą z nich jest wybór sposobu kodowania rozwiązań na materiale genetycznym osobników wchodzących w skład populacji, a drugą jest określenie postaci funkcji dopasowania, która w procesie selekcji posłuży do oceny proponowanych przez poszczególne osobniki rozwiązań, umożliwiając tym samym realizację idei darwinowskiego doboru naturalnego [11–15].
Obecnie algorytmy ewolucyjne stanowią powszechnie już uznaną technikę obliczeniową, która z powodzeniem wykorzystywana jest do rozwiązywania różnych kategorii problemów optymalizacyjnych oraz symulacji przebiegu procesów ewolucyjnych obserwowanych w przyrodzie [16–20]. Z tego powodu spodziewać się należy ich równie wysokiej skuteczności w rozważanym w artykule obszarze alokacji i szeregowania zadań
W przypadku zaimplementowanego przez autora systemu przyjęto sposób kodowania rozwiązań oparty na liczbach naturalnych. Mianowicie z każdym genem osobnika zostało skojarzone jedno zadanie periodyczne podlegające procesowi alokacji, przy czym przyjęto, że liczba naturalna zapisana na danym genie koduje bezpośrednio numer procesora, do którego skojarzone z nim zadanie zostanie przydzielone. Jak widać, poszczególne geny wszystkich osobników mogą przybierać jedynie wartości będące liczbami naturalnymi z przedziału od jeden do pięciu.
Z kolei wartość funkcji dopasowania f wyznaczana jest za pomocą algorytmu określonego w postaci następującego pseudokodu:
1. Funkcji dopasowania przypisz wartość równą zero f = 0;
2. Jeżeli w przypadku procesora nr 1 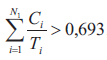
3. Jeżeli w przypadku procesora nr 2 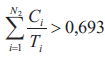
4. Jeżeli w przypadku procesora nr 3 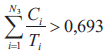
5. Jeżeli w przypadku procesora nr 4 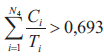
6. Jeżeli w przypadku procesora nr 5 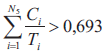
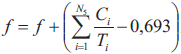
Jak wynika z postaci przedstawionej powyżej procedury pozwalającej na wyznaczenie wartości funkcji dopasowania, w rozważanym przypadku funkcja dopasowania przybiera postać funkcji kary, która nakładana jest za przekroczenie w wypadku poszczególnych procesorów warunku wystarczającego na szeregowalność przydzielonych do nich podzbiorów zadań, który zadany jest nierównością (2). Jedynie w przypadku, gdy w ramach wszystkich procesorów systemu heterogenicznego spełniona jest nierówność (2), wówczas funkcja dopasowania przyjmuje wartość równą zero. We wszystkich innych przypadkach funkcja dopasowania przybiera wartości dodatnie, w związku z czym celem algorytmu ewolucyjnego jest minimalizacja wartości funkcji dopasowania poprzez cykliczne wykonywanie operacji mutacji i selekcji, aż funkcja dopasowania osiągnie wartość równą zero, co oznacza spełnienie warunku wystarczającego do każdego z procesorów rozważanego systemu heterogenicznego.
W przypadku zaimplementowanego algorytmu ewolucyjnego operacja selekcji została zrealizowana w postaci selekcji turniejowej, która polegała na tym, że osobniki były łączone w sposób losowy w pary, a następnie z każdej takiej pary do kolejnego pokolenia przechodził jedynie osobnik lepiej dopasowany, czyli taki, którego funkcja dopasowania miała mniejszą wartość. Przyjęcie przez funkcję dopasowania wartości zero, oznaczało odnalezienie poszukiwanego rozwiązania, czyli takiego, w przypadku którego warunek konieczny na szeregowalność zbioru zadań periodycznych był spełniony w przypadku każdego z procesorów wchodzących w skład systemu heterogenicznego.
W efekcie zastosowanie algorytmu ewolucyjnego doprowadziło do odnalezienia następującego schematu alokacji zadań dla poszczególnych procesorów systemu heterogenicznego, którego szczegóły zostały przedstawione w tabeli.
| Zadanie | Okres zadania [ms] | Czas realizacji zadania w przypadku procesora nr 1 [ms] | Numer procesora, do którego przydzielone zostało dane zadanie |
| z1 | 3400 | 340 | 3 |
| z2 | 9800 | 980 | 4 |
| z3 | 6800 | 130 | 5 |
z4 | 13900 | 190 | 5 |
| z5 | 2700 | 270 | 3 |
| z6 | 8700 | 870 | 2 |
| z7 | 5200 | 520 | 5 |
| z8 | 8900 | 800 | 1 |
| z9 | 6300 | 630 | 3 |
| z10 | 5100 | 510 | 5 |
| z11 | 6300 | 165 | 1 |
| z12 | 12900 | 245 | 5 |
| z13 | 8600 | 230 | 3 |
| z14 | 6200 | 310 | 1 |
| z15 | 11400 | 370 | 5 |
| z16 | 8900 | 105 | 2 |
| z17 | 9900 | 465 | 5 |
| z18 | 3900 | 195 | 1 |
| z19 | 5800 | 190 | 3 |
| z20 | 4600 | 130 | 1 |
| z21 | 13600 | 340 | 2 |
| z22 | 9900 | 280 | 2 |
| z23 | 11500 | 140 | 3 |
| z24 | 2900 | 190 | 1 |
| z25 | 12800 | 270 | 1 |
| z26 | 8900 | 180 | 3 |
| z27 | 5400 | 520 | 4 |
| z28 | 8200 | 160 | 5 |
| z29 | 16500 | 230 | 2 |
| z30 | 5300 | 330 | 3 |
| z31 | 7600 | 340 | 2 |
| z32 | 9900 | 580 | 1 |
| z33 | 1400 | 130 | 3 |
| z34 | 4900 | 190 | 1 |
| z35 | 6800 | 270 | 4 |
| z36 | 8800 | 390 | 4 |
| z37 | 7300 | 420 | 4 |
| z38 | 8400 | 840 | 2 |
| z39 | 6700 | 630 | 2 |
| z40 | 10500 | 420 | 3 |
| z41 | 25600 | 320 | 4 |
| z42 | 9800 | 920 | 4 |
| z43 | 1800 | 130 | 5 |
| z44 | 1900 | 140 | 2 |
| z45 | 2900 | 240 | 5 |
| z46 | 3800 | 230 | 1 |
| z47 | 5200 | 510 | 4 |
| z48 | 8600 | 800 | 1 |
| z49 | 6300 | 610 | 2 |
| z50 | 5600 | 510 | 1 |
W wyniku realizacji algorytmu ewolucyjnego otrzymano następujące wartości stopni wykorzystania poszczególnych procesorów wchodzących w skład badanego sytemu heterogenicznego:
Rys. 1. Ilustracja sposobu dochodzenia do stabilnego rozwiązania w przypadku procesora nr 1:
Rys. 2. Ilustracja sposobu dochodzenia do stabilnego rozwiązania w przypadku procesora nr 2:
Rys. 3. Ilustracja sposobu dochodzenia do stabilnego rozwiązania w przypadku procesora nr 3:
Rys. 4. Ilustracja sposobu dochodzenia do stabilnego rozwiązania w przypadku procesora nr 4:
Rys. 5. Ilustracja sposobu dochodzenia do stabilnego rozwiązania w przypadku procesora nr 5:
Jak widać, w przypadku każdego z rozważanych procesorów spełniony jest warunek wystarczający na szeregowalność przydzielonego do niego podzbioru zadań, zadany nierównością (2), ponieważ stopień wykorzystania tych procesorów nie przekracza wartości 0,693. Ponadto wartym zwrócenia uwagi jest fakt w miarę równomiernego obciążenia wszystkich procesorów, ponieważ ich stopnie wykorzystania mają bardzo zbliżone wartości.
Dodatkowo za pomocą wykresów przedstawionych na rys. 1–5 zilustrowano sposób dochodzenia algorytmu ewolucyjnego do stabilnych rozwiązań końcowych. Jak wynika z wykresów zamieszczonych na rys. 1–5, stabilne rozwiązania uzyskiwane są po upływie już kilkudziesięciu pokoleń algorytmu ewolucyjnego, w związku z czym jego zbieżność jest bardzo szybka.
Ponadto analizując wykresy zamieszczone na rys. 1–5, wyróżnić można dwa odmienne sposoby dochodzenia algorytmu ewolucyjnego do stabilnych rozwiązań. W przypadku pierwszego z nich, który charakterystyczny jest dla procesorów nr 1 i 4, stopień wykorzystania procesora zmienia się w sposób monotoniczny, dochodząc asymptotycznie do wartości końcowej. W przypadku procesora nr 1 jego stopień wykorzystania narasta od wartości początkowej, równej 0,518, do wartości końcowej, równej 0,673. Z kolei w przypadku procesora nr 4 jego stopień wykorzystania maleje, począwszy od wartości początkowej, równej 0,932, do wartości końcowej, równej 0,678. Natomiast w przypadku wykresów odnoszących się do procesorów nr 2, 3 i 5 zaobserwować można charakterystyczne oscylacje, podczas których wartość stopnia wykorzystania tych procesorów gwałtownie wzrasta w początkowej fazie realizacji algorytmu ewolucyjnego, by następnie asymptotycznie zmaleć do stabilnej wartości końcowej.
Reasumując zawarte w artykule rozważania, należy stwierdzić, że technika obliczeniowa oparta na zastosowaniu algorytmów ewolucyjnych może zostać z powodzeniem użyta w celu realizacji zagadnienia optymalizacji rozdziału zadań periodycznych w heterogenicznych systemach wieloprocesorowych. W rozważanym wypadku zastosowanie algorytmu ewolucyjnego prowadzi do odnalezienia takich schematów alokacji zadań periodycznych, w przypadku których dla każdego z procesorów spełniony jest warunek wystarczający na szeregowalność przydzielonego do niego podzbioru zadań. Dodatkowo algorytm ewolucyjny gwarantuje taki przydział zadań, który odznacza się zrównoważeniem stopnia obciążenia wszystkich procesorów systemu heterogenicznego.
[1] Shin K. G., Ramanathan P.: Real-time computing: A new discipline of computer science and engineering, Proceedings of the IEEE, vol. 82, 1994, ss. 6–24.
[2] Hsueh W., Lin K. J.: Scheduling real-time systems with end-to-end timing constraints using the distributed pinwheel model, IEEE Transactions on Computers, vol. 50, 2001, ss. 51–67.
[3] Lala J. H., Harper R. E.: Architectural principles for safety-critical real-time applications, Proceedings of the IEEE, vol. 82, 1994, ss. 25–41.
[4] Szmuc T., Motet G.: Specyfikacja i projektowanie oprogramowania czasu rzeczywistego, Wydawnictwa CCATIE, Kraków 1998
[5] Suri N., Hugue M. M., Walter C. J.: Synchronization issues in realtime systems, Proceedings of the IEEE, vol. 82, 1994, ss. 41–53.
[6] Stoyenko T., Baker P.: Real-time schedulability analyzable mechanisms in Ada9X, Proceedings of the IEEE, vol. 82, 1994, ss. 95–107.
[7] Ramamrithan K., Stankovic J. A.: Scheduling algorithms and operating systems support for real-time systems, Proceedings of the IEEE, vol. 82, 1994, ss. 55–67.
[8] Sha L., Rajkumar R., Sathaye S. S.: Generalized rate-monotonic scheduling theory: A framework for developing real-time systems, Proceedings of the IEEE, vol. 82, 1994, ss. 68–82.
[9] Tannenbaum A.: Rozproszone systemy operacyjne, WNT, Warszawa, 1996
[10] Coulouris G., Dollimore J., Kindberg T.: Systemy rozproszone – podstawy i projektowanie, WNT, Warszawa, 1998.
[11] Goldberg D. E.: Algorytmy genetyczne i ich zastosowania, Wydawnictwa Naukowo-Techniczne, Warszawa 1996.
[12] Arabas J.: Wykłady z algorytmów ewolucyjnych, Wydawnictwa Naukowo-Techniczne, Warszawa 2004.
[13] Rutkowska D.: Inteligentne systemy obliczeniowe i sztuczna inteligencja, [w] Biocybernetyka i inżynieria biomedyczna 2000, pod redakcją Macieja Nałęcza, Tom 6 – Sieci neuronowe, ss. 765–784.
[14] Michalewicz Z.: Algorytmy genetyczne + struktury danych = programy ewolucyjne, Wydawnictwa Naukowo-Techniczne, Warszawa 2003.
[15] Rutkowska D., Piliński M., Rutkowski L.: Sieci neuronowe, algorytmy genetyczne i systemy rozmyte, Wydawnictwo Naukowe PWN, Warszawa – Łódź 1997.
[16] Gras R., Devaurs D., Wozniak A., Aspinall A.: An individual-based evolving predator-prey ecosystem simulation using a fuzzy cognitive map as the behavior model, Artificial Life, vol. 15, 2009, ss. 423–463.
[17] Bullinaria J. A.: Lifetime learning as a factor in life history evolution, Artificial Life, vol. 15, 2009, ss. 389–409.
[18] Stanley K. O., A’Ambrosio D. B., Gauci J.: A hypercube-based encoding for evolving large-scale neural networks, Artificial Life, vol. 15, 2009, ss. 185–212.
[19] Ampatzis C., Tuci E., Trianni V., Christensen A. L., Dorigo M.: Evolving self-assembly in autonomous homogeneous robots: Experiments with two physical robots, Artificial Life, vol. 15, 2009, ss. 465–484.
[20] Paenke I., Kawecki T. J., Sendhoff B.: The influence of learning on evolution: A mathematical framework, Artificial Life, vol. 15, 2009, ss. 227–245.
| REKLAMA |

| REKLAMA |