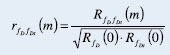Analiza wyników pomiaru dopplerowskiego przesunięcia częstotliwości

Miarą oceny skuteczności przedstawionej metody eliminacji błędów anomalnych są właściwości korelacyjne, jakie występują odpowiednio dla wartości pomiarowych i teoretycznych. Teoretyczna wartość dopplerowskiego przesunięcia częstotliwości jest wyznaczana na podstawie parametrów układu pomiarowego za pomocą zależności opisanej poniższym wzorem [1]:

gdzie:
f_Dt(x,t) – wartość dopplerowskiego przesunięcia częstotliwości;
f(x,t) – wartość chwilowa częstotliwości (częstotliwość
odbieranego sygnału);
f₀ – częstotliwość nadawanego sygnału;
v – prędkość przemieszczania się nadajnika;
k=(v/c),c– prędkość propagacji fali elektromagnetycznej
w ośrodku;
x,y,z – współrzędne punktu położenia anteny odbiorczej.

Dotychczasowe rozważania dotyczyły wykorzystania przedstawionej metodyki do eliminacji błędów anomalnych znacznie zaburzający charakter odbieranego sygnału. Za pomocą opisanej metody możliwe jest również usunięcie z sygnału wyników pomiarowych o mniejszej dynamice zmian wartości chwilowych częstotliwości. Odbywa się to poprzez zmianę wartości przyjętego kryterium za pomocą odpowiedniego mnożnika oznaczonego jako l. Dla wartości mnożnika mniejszej od 1 z sygnału usuwane są punkty pomiarowe o dynamice zmian wartości chwilowej mniejszej niż w przypadku błędów anomalnych. Z kolej jeżeli wartość mnożnika jest odpowiednio większa od 1, sygnał pozostaje niezmieniony bądź usuwane są z niego tylko najbardziej znaczące błędy anomalne.

W związku z powyższym powstało pytanie, dla jakiej wartości przyjętego mnożnika metoda eliminacji błędów jest najskuteczniejsza, czyli kiedy występuje największe skorelowanie pomiędzy krzywą teoretyczną i pomiarową? Aby na nie odpowiedzieć analizie poddano wyniki czterech pomiarów różniących się dynamiką zmian wartości chwilowych częstotliwości. Dla każdego z pomiarów wartości mnożnika dobierano tak, aby zaobserwować kolejne etapy eliminacji błędów.



W celu określenia optymalnego zakresu zmienności mnożnika, dla którego wartości pomiarowe są najbliższe teorii, została przeprowadzona analiza ich właściwości korelacyjnych.

Doprowadziło to do wyznaczenia zależności końcowej stanowiącej miarę podobieństwa analizowanych wartości:

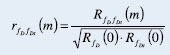
Przeprowadzone w podany sposób normowanie funkcji korelacji wzajemnej zapobiega pojawieniu się pozornie wysokich wartości korelacji wynikających z poziomu dynamicznych zmian wyników pomiarowych. Pozwala to więc na określenie podobieństwa analizowanych przebiegów ze względu na ich ogólny charakter, bez wpływu wartości dynamicznych zmian wyników pomiarowych.

Wyniki analizy korelacyjnej przeprowadzonej dla czterech pomiarów pozwalają na ogólne wyznaczenie zakresu wartości, jakie powinien przyjmować przedstawiony wcześniej mnożnik, aby zbiór końcowych wartości pomiarowych był jak najbliższy teorii.

Wykresy przedstawiają zależność maksymalnych wartości unormowanej korelacji wzajemnej w funkcji mnożnika l. Jak wynika z charakterystyk, gwałtowny wzrost korelacji następuje dla wartości mnożnika z zakresu 10-20, ponieważ wtedy zastępowane są wyniki pomiarowe odpowiadające błędom anomalnym o największym poziomie. Dla l mniejszych od 10 korelacja liniowo narasta, ze względu na stopniową eliminację z wartości pomiarowych błędów anomalnych o niższych poziomach. Liniowe narastanie utrzymuje aż do wartości l≈1, kiedy to następuje wzrost korelacji związany z usunięciem wszystkich błędów anomalnych. Dalsze zmniejszanie wartości mnożnika prowadzi do całkowitej eliminacji dynamicznych zmian częstotliwości i zastąpienia ich krzywą kosinusoidalną. Dzieje się tak z powodu minimalizacji kryterium decydującego o anomalności, co powoduje, że wszystkie zmiany dynamiczne są uznawane za anomalne i nie można zastąpić ich wartością średnią z sąsiednich wyników pomiarowych. Dla każdego z czterech analizowanych pomiarów sytuacja taka następuje dla wartości mnożnika bliskiej 0,5 i pozostaje bez zmian dla pozostałych wartości dążących do 0.

Okazuje się, że właśnie w tym zakresie mnożnika l funkcja korelacji wzajemnej przyjmuje wartości maksymalne, co oznacza, że krzywa kosinusoidalna określona do celów eliminacji błędów anomalnych w optymalny sposób aproksymuje wartości pomiarowe. Wynika z tego więc, że krzywa wyznaczona w prosty sposób na podstawie danych pomiarowych dość dobrze oddaje charakter odbieranego sygnału. Z punkty widzenia analizy podstawowych parametrów dopplerowskiego przesunięcia częstotliwości, takich jak maksymalna wartość przesunięcia lub moment jego zerowania, aproksymacja wyznaczoną krzywą kosinusoidalną jest w większości przypadków wystarczająca. W sytuacji natomiast, gdy analiza dotyczy również ściśle określonych zmian dynamicznych, nie można wykorzystać aproksymacji krzywą kosinusoidalną ponieważnie oddaje ona ich charakteru.


Przeprowadzona na podstawie wartości pomiarowych i teoretycznych analiza bazująca na korelacyjnych właściwościach porównywanych danych pokazuje skuteczność opracowanej metody eliminacji błędów anomalnych, dzięki której następuje znaczna poprawa dokładności lokalizacji źródeł emisji fal radiowych. Poprzez dobór odpowiedniej wartości kryterium określającego stopień anomalności możliwa jest regulacja zakresu eliminacji błędów. Istnieją stałe przedziały wartości mnożnika skalującego wybrane kryterium, dla których wyniki analizy korelacyjnej przyjmują określony charakter. W trakcie analizy okazało się, że można z dobrym skutkiem aproksymować wartości chwilowe częstotliwości odebranego sygnału za pomocą krzywej kosinusoidalnej wyznaczonej w prosty sposób na podstawie danych pomiarowych.

autor:Kamil Bechta

Literatura
[1] Ziółkowski C.: Zjawisko Dopplera w systemach radiokomunikacji mobilnej, KKRRiT’2005, Kraków, 15-17 czerwca 2008
[2] Ziółkowski C., Rafa J., Kelner J. M.: Lokalizacja źródeł fal radiowych na podstawie sygnałów odbieranych przez ruchomy odbiornik pomiarowy, Biuletyn WAT, numer specjalny 2006, Warszawa, str. 67-82
[3] Kelner J.M.: Praktyczna ocena możliwości lokalizacji źródeł emisji radiowych na podstawie dopplerowskiego przesunięcia częstotliwości, KKRRiT’2008, Wrocław, 9-11 kwietnia 2008
[4] Kachel L., Ziółkowski C., Kelner J. M., Fabianiak R.: Stanowisko do pomiaru zmian częstotliwości odbieranego sygnału przez ruchome urządzenie odbiorcze, KKRRiT’2008, Wrocław, 9-11 kwietnia 2008